圖解克希荷夫電流與電壓定律

本文用三個例子說明電路學當中的基本且重要的定律：克希荷夫電路定律（Kirchhoff’s circuit laws）。這個定律分成電壓和電流兩個定律，用於分析電路的電流以及元件兩端的電位。

例一：推導R1和R2電阻的並聯值公式。

在電子迴路中，進入任何節點的總電流等於離開該節點的總電流，這項法則稱為克希荷夫電流定律（Kirchhoff’s Current Law, 簡稱KCL）。

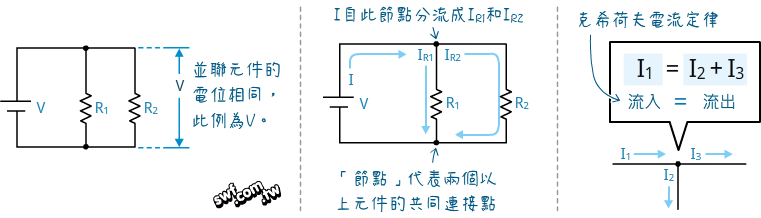
將歐姆定律I=V/R，帶入克希荷夫電流定律，即可推導出並聯電組公式：

例二：求底下電路中的I₂和I₃電流值。

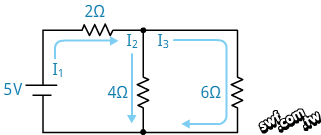
分析這個電路需要用到克希荷夫電壓定律（Kirchhoff’s Voltage Law，簡稱KVL）和電流定律。克希荷夫電壓定律指出，環繞任何封閉迴路的所有電位差（電壓）總和等於0。先瞧瞧底下的電路：

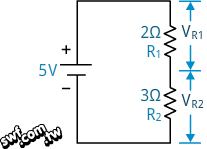
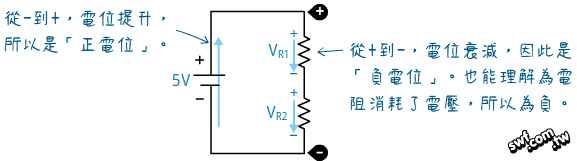
串聯電阻兩端的電位，等於電源電壓。電阻會造成電壓降，在算式中是「負電位」，因為它消耗了電能，所以迴路中的電位差總合為0。

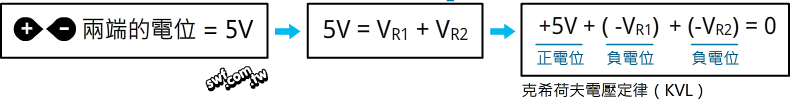
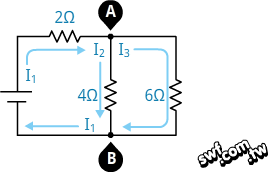
回到例二開頭的電路，其電流在節點處一分為二，有兩個封閉迴路，我們要單獨分析每個封閉迴路。

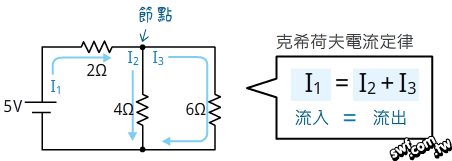
先處理左邊的封閉迴路：

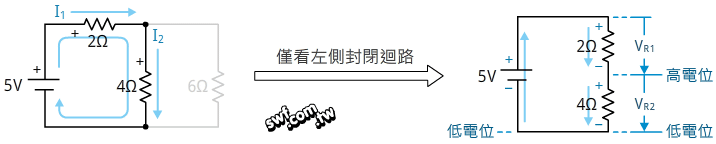
VR1與VR2電位的總和，等於電源5V，因此：

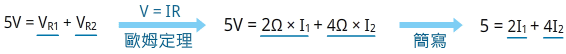
上面的式子有兩個未知數I₁和I₂，因此還無法求出它們的值。現在，分析右側封閉迴路，假設電流在其中以順時針方向流動：

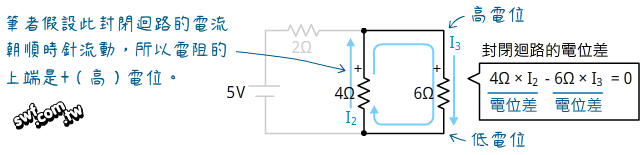
根據克希荷夫電壓定律，可求出I₂和I₃的關係：

以上是「假設電流朝順時針流動」，我們也可以假設電流朝「逆時針」流動，像底下的算法，最終結果相同。

取得I₂，再回頭看左側的封閉迴路，用I₂+I₃取代I₁：

5 = 2I₂ + 2I₃ + 4I₂
5 = 6I₂ + 2I₃

再用1.5 I₃取代I₂，便能得知I₃約為0.4545A：

這樣就能算出I₂和I₁的值：

例三：驗證問題二的計算結果。首先計算迴路的總電阻值，再藉此求出電流：

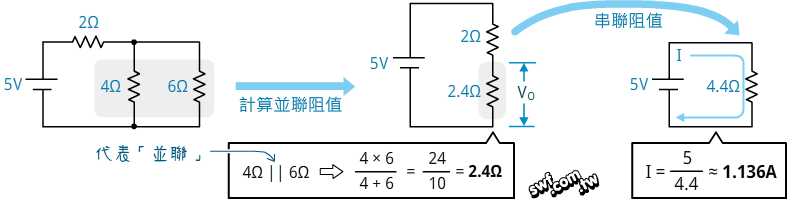
上圖左的計算式求出的電流I為1.136A，跟上一節的I₁值一致。從下圖可看出，電流I₁在節點A分流成I₂和I₃、並於節點B匯流成I₁，因此I1值就是上圖右的I值。

電路裡的4Ω和6Ω並聯，其等效值為2.4Ω。在2Ω和2.4Ω的分壓值VO約為2.7272V：

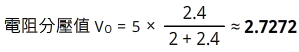
根據歐姆定律V=IR，帶入上一節求得的I₂=0.6818，可計算出4Ω電阻的電位差約莫2.7272V，跟上面的計算結果相同，因此可證明上一節的I₂值也是正確的。

4Ω電阻的電位差 → 4Ω × I₂ → 4 × 0.6818 = 2.7272

輸入阻抗影響訊號的電路分析

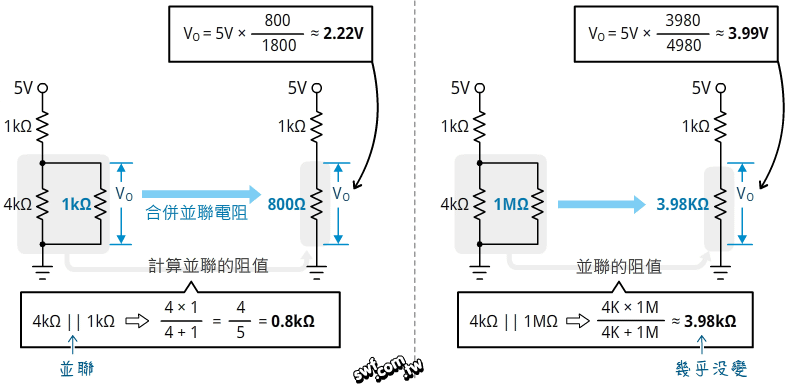
元件的輸入阻抗會影響輸入訊號。尚未連接元件時，下圖左的VO分壓為4V；分別連接輸入阻抗為1KΩ和1MΩ的元件，分壓VO會不同嗎？

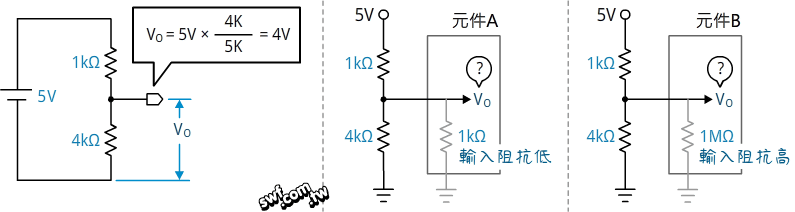
從底下的算式可知，輸入阻抗越低，輸入訊號衰減的越嚴重。微控器的類比輸入埠的輸入阻抗通常都有好幾MΩ，所以《超圖解Arduino互動設計入門》第8章的光敏電阻分壓訊號幾乎不受影響。